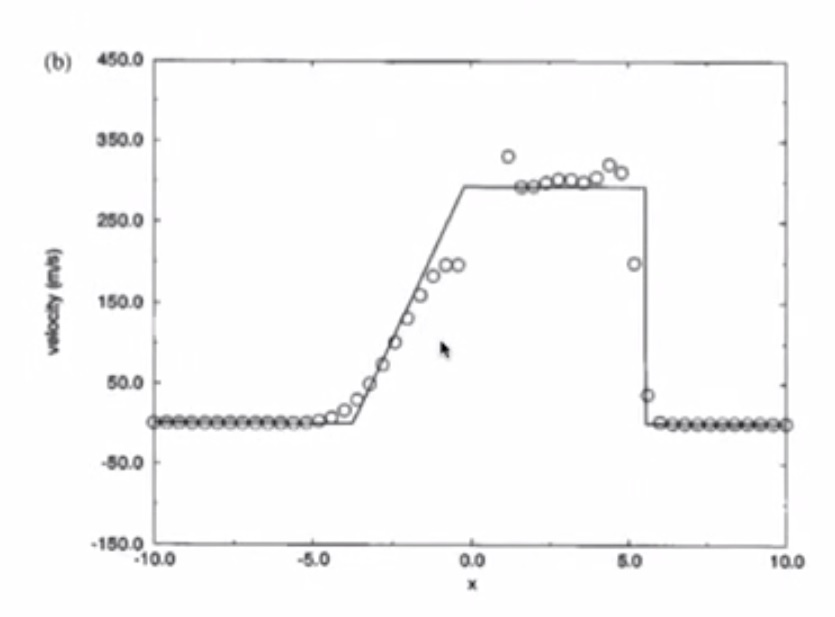
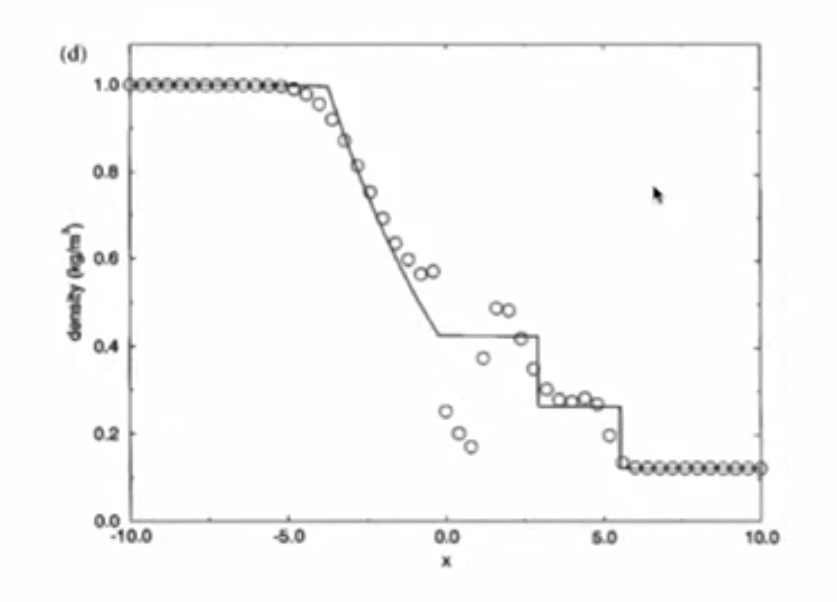
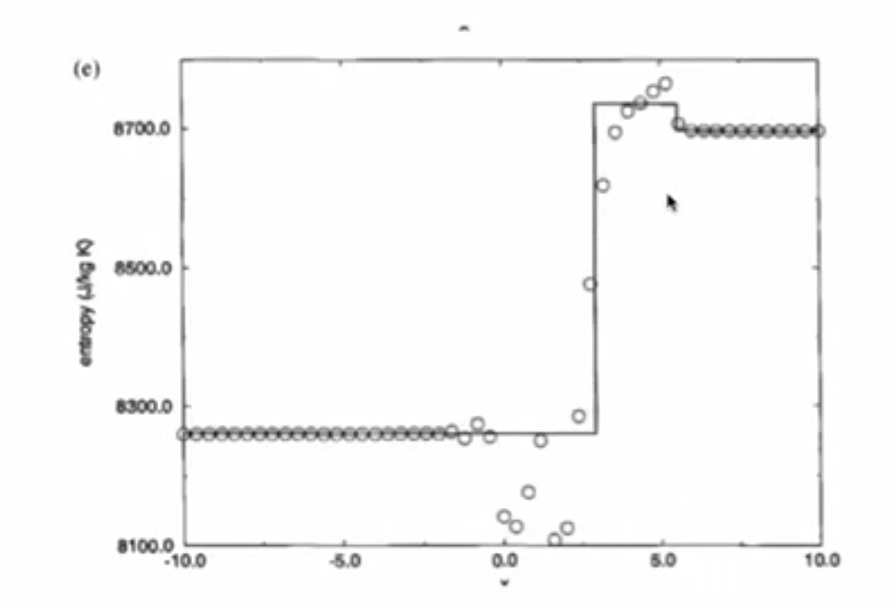
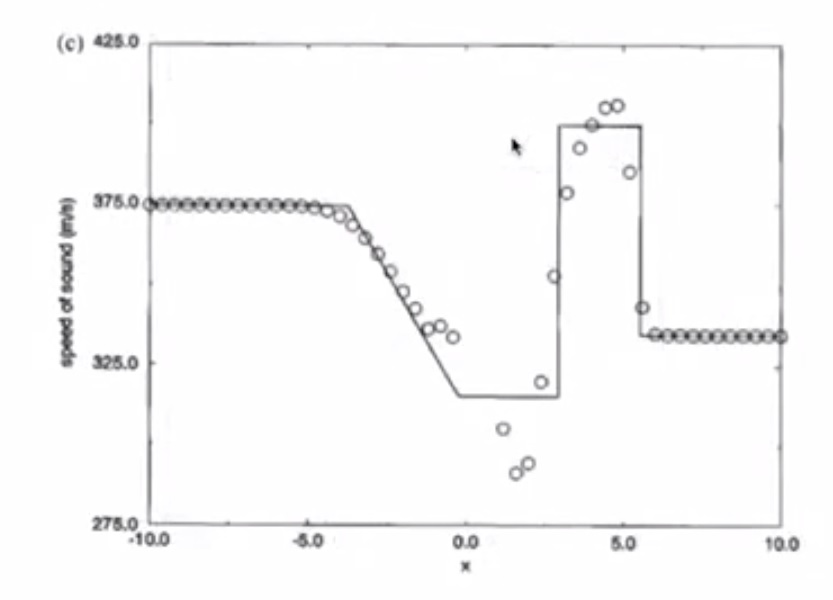
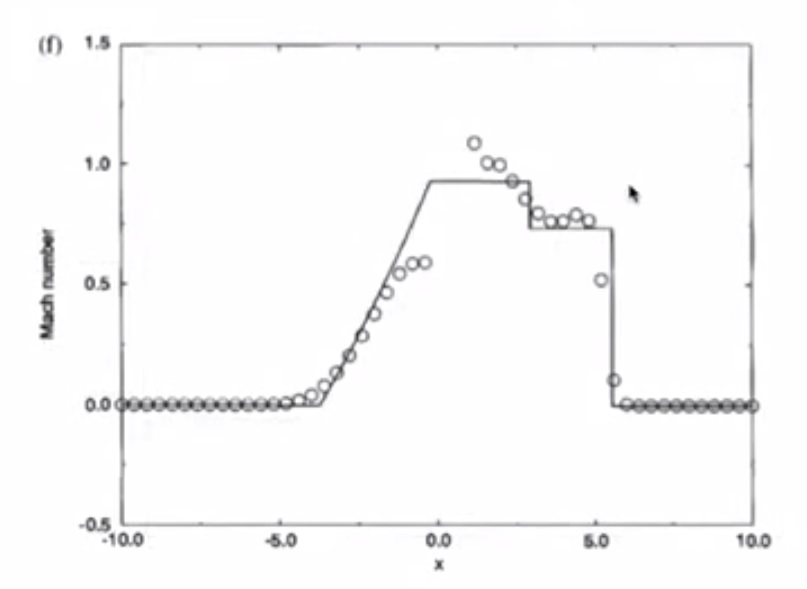
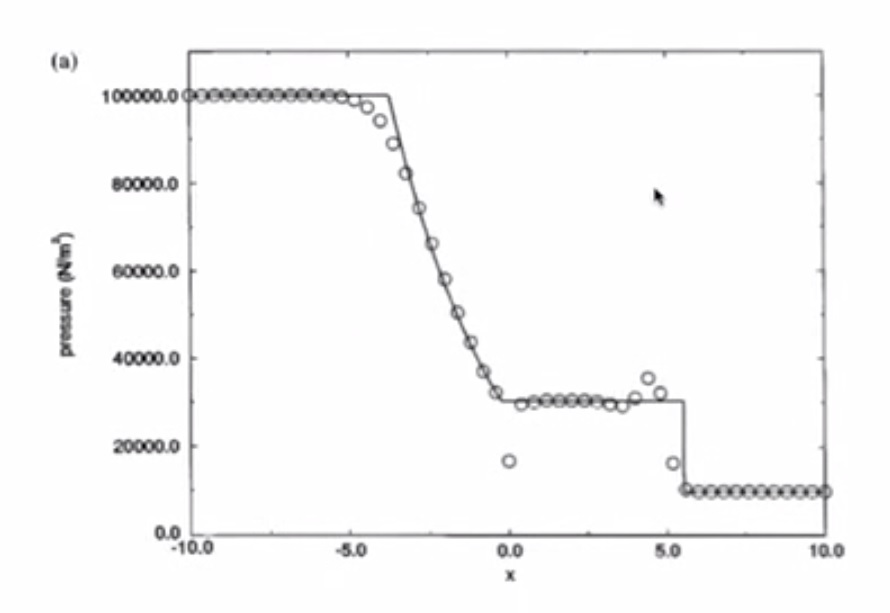
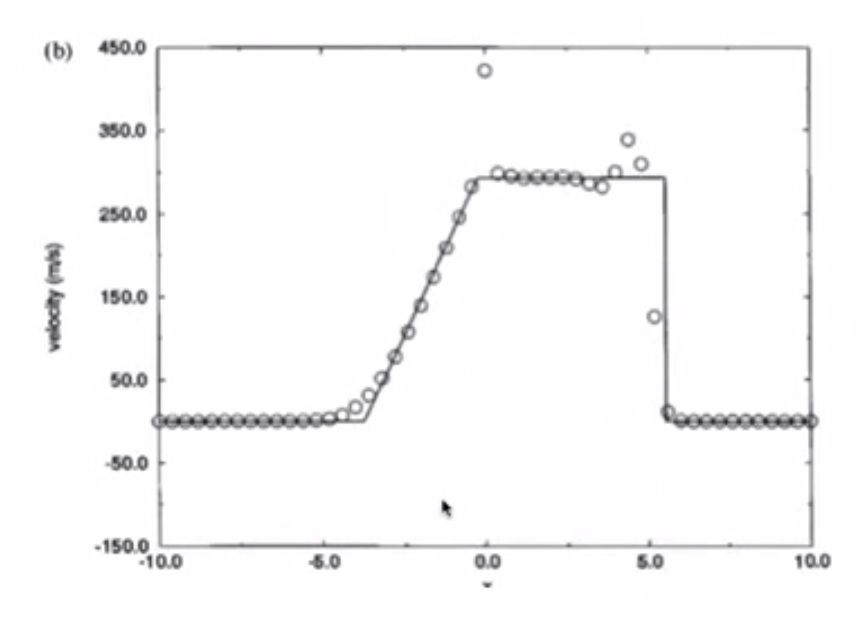
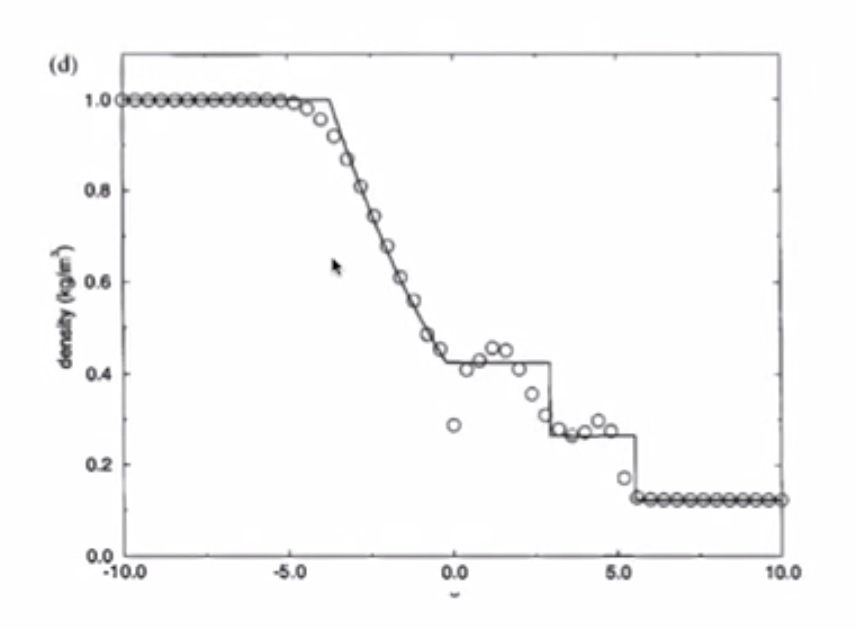
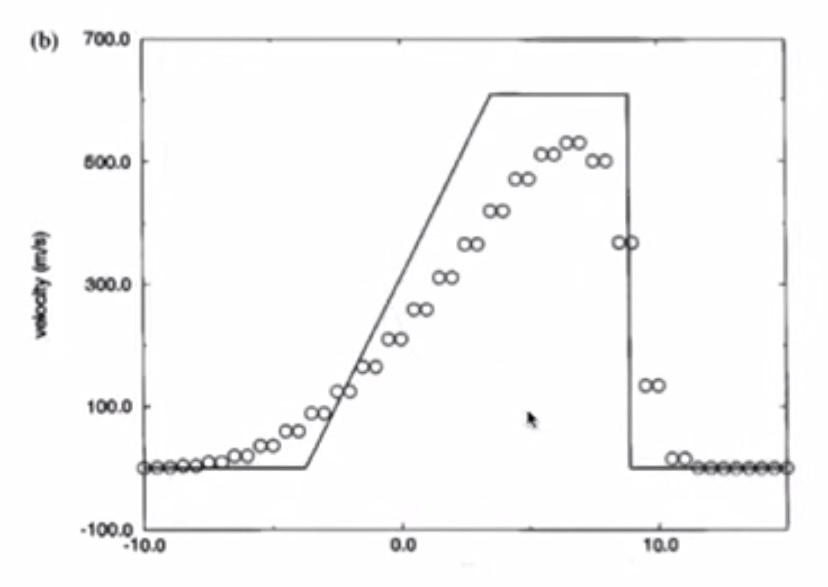
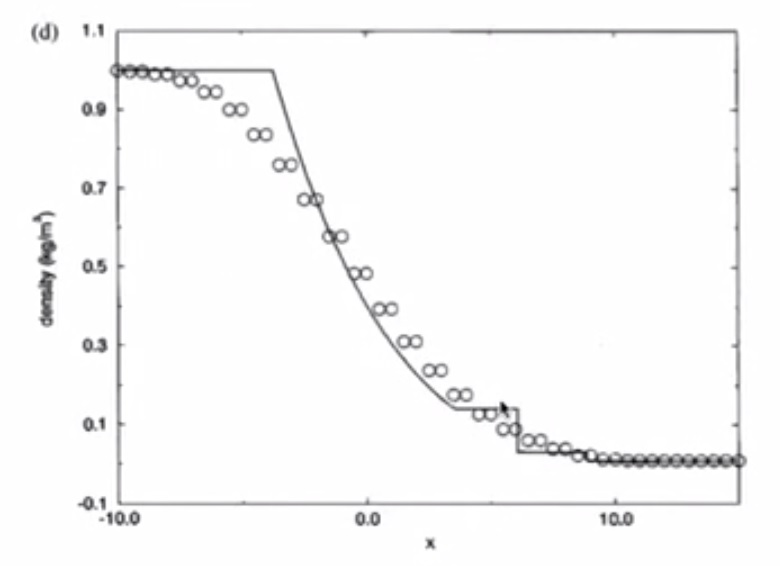
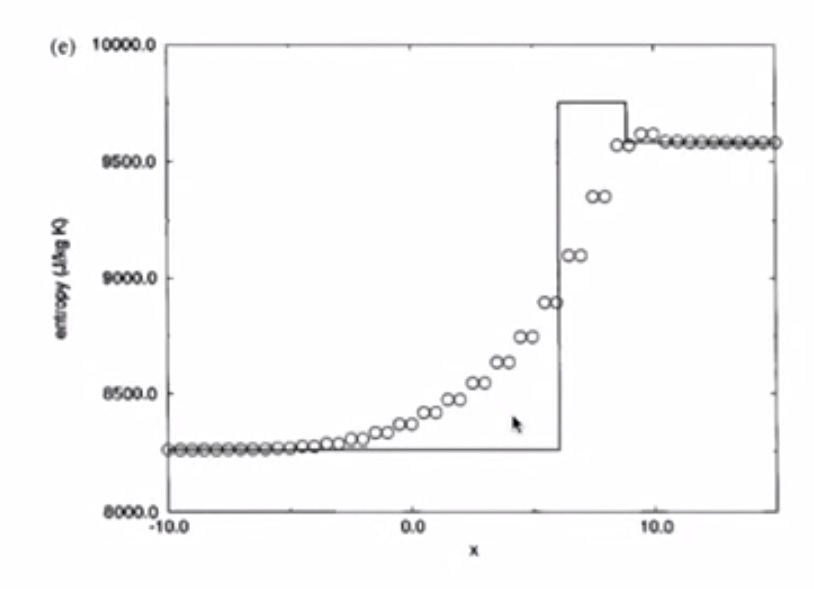
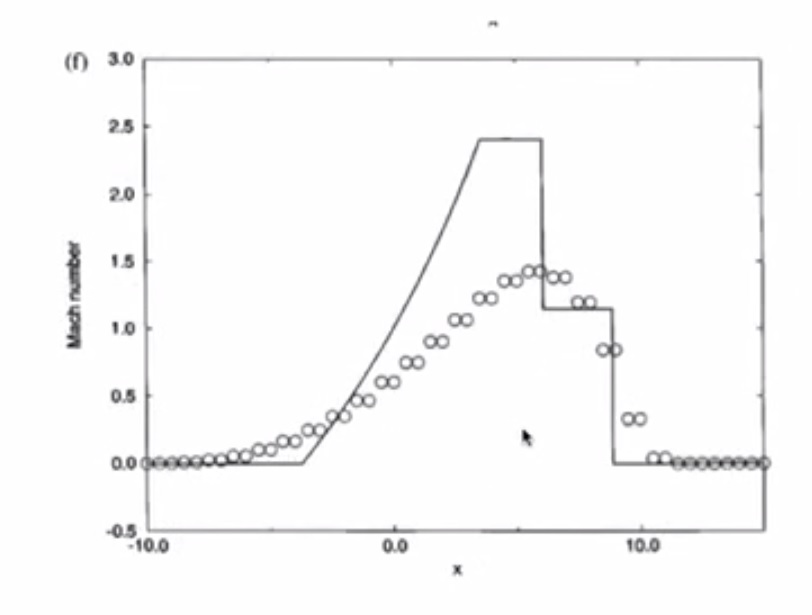
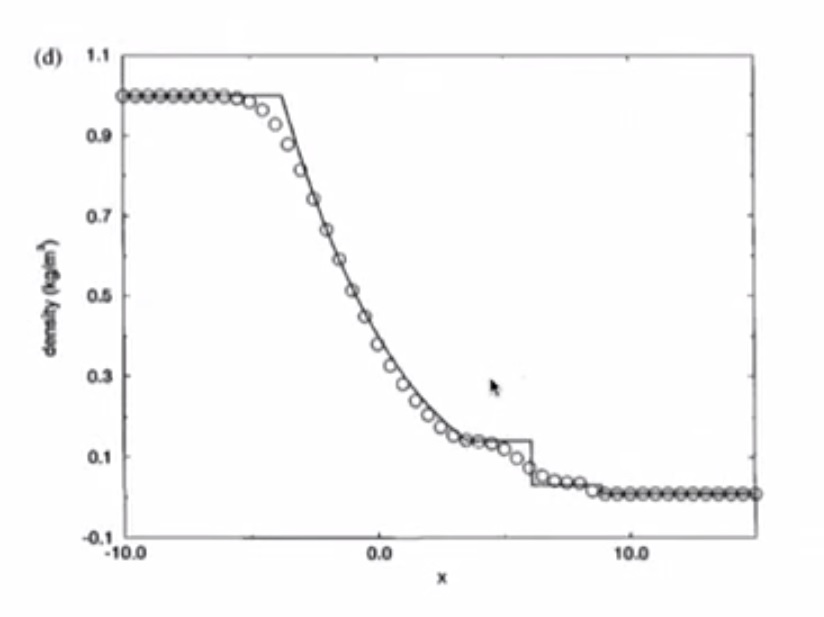
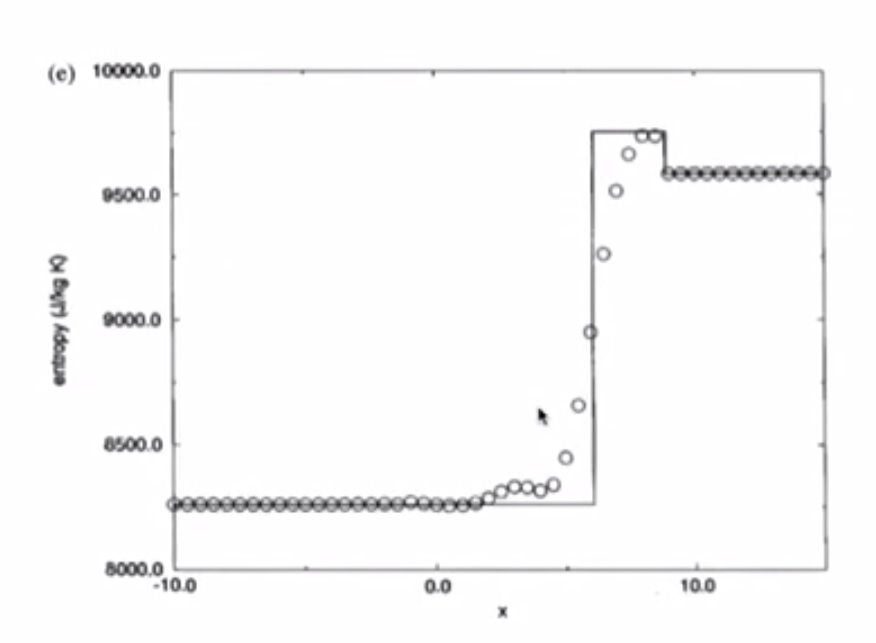
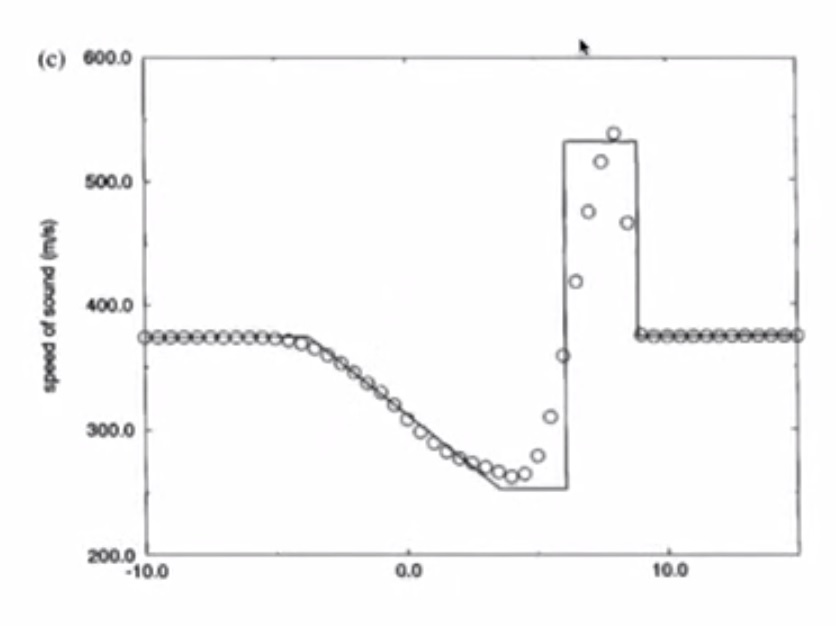
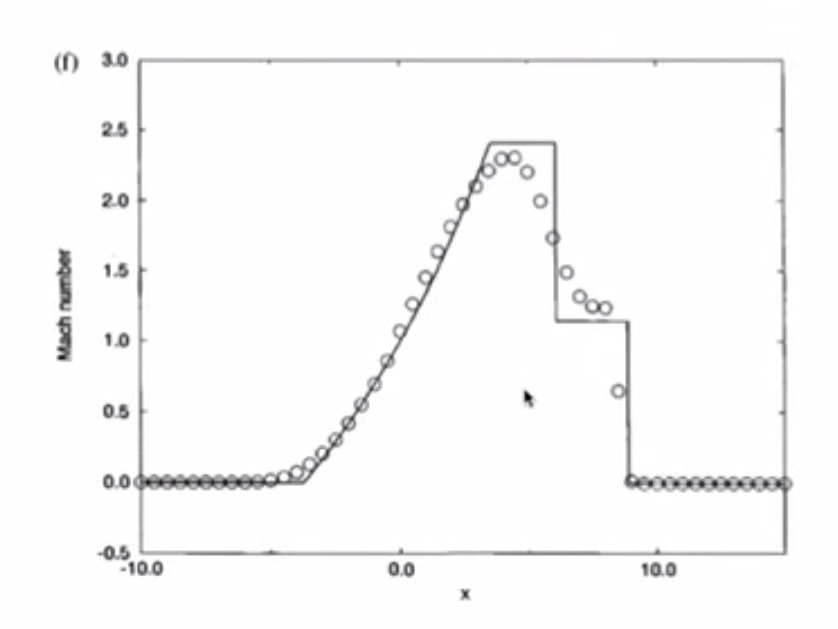
4. Sod’s Test Problems: The Shock Tube Problem¶
This set of problems was introduced in the paper by Gary Sod in 1978 called “A Survey of Several Finite Difference Methods for Systems of Non-linear Hyperbolic Conservation Laws”
4.1. Assumptions¶
- 1D
- Infinitely long tube
- Inviscid fluid
4.2. Initial Conditions¶
- At t=0 the diaphragm is instantaneously removed (this is done experimentally using a a thin sheet of metal and a small explosion bursts the diaphragm)
4.3. Regions of Flow¶
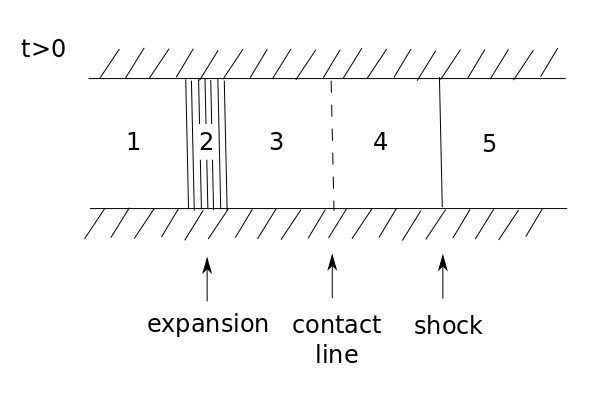
- The bursting of the diaphragm causes a 1D unsteady flow consisting of a steadily moving shock - A Riemann Problem.
- 1 discontinuity is present
- The solution is self-similar with 5 regions
- Region 1 & 5 - left and right sides of initial states
- Region 2 - expansion or rarefaction wave (x-dependent state)
- Regions 3 & 4 - steady states independent of x within the region (uniform)
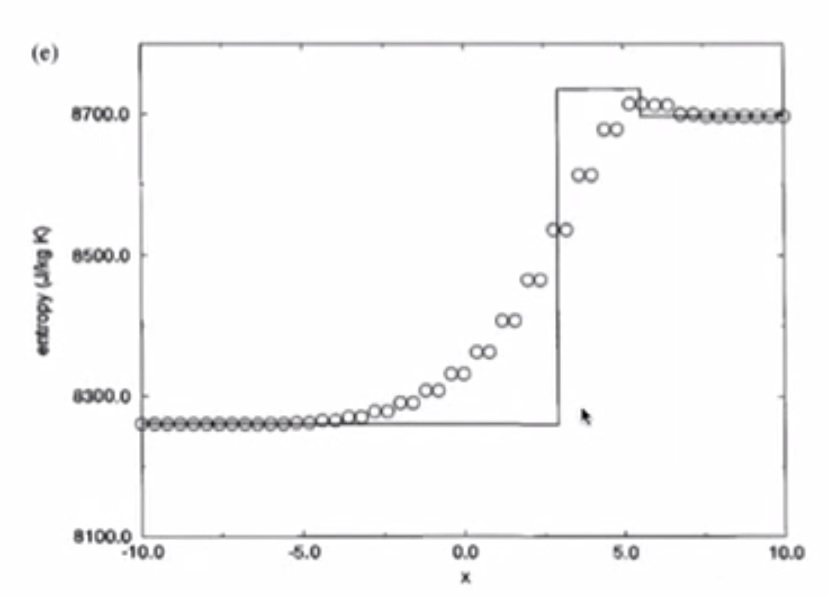
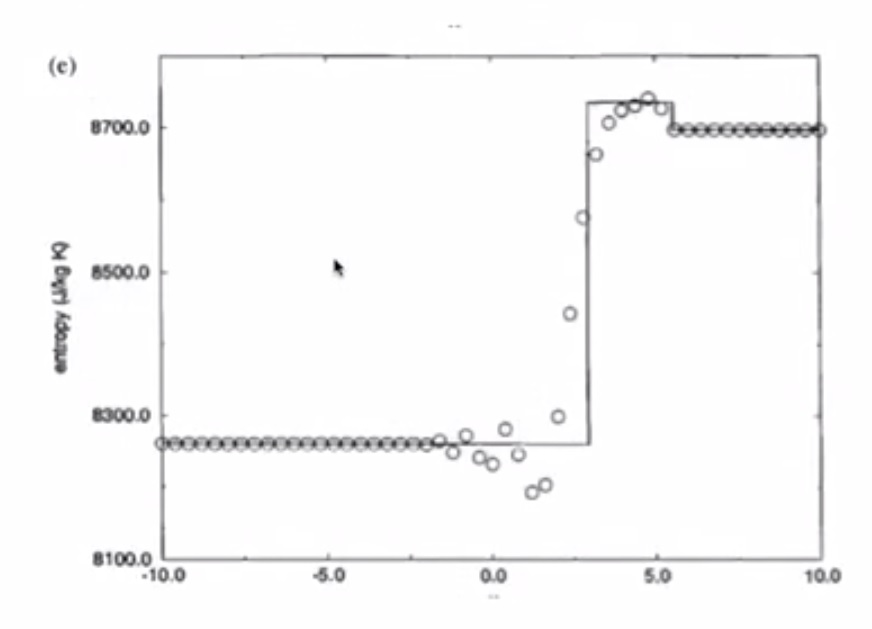
Contact line between 3 and 4 separates fluids of different entropy (but they have the same pressure and velocity) i.e. it’s an invisible line - e.g. two fluids one side with water and the other with dye - contact line is moving.
4.4. Sod’s Test Number 1¶
Unknowns:
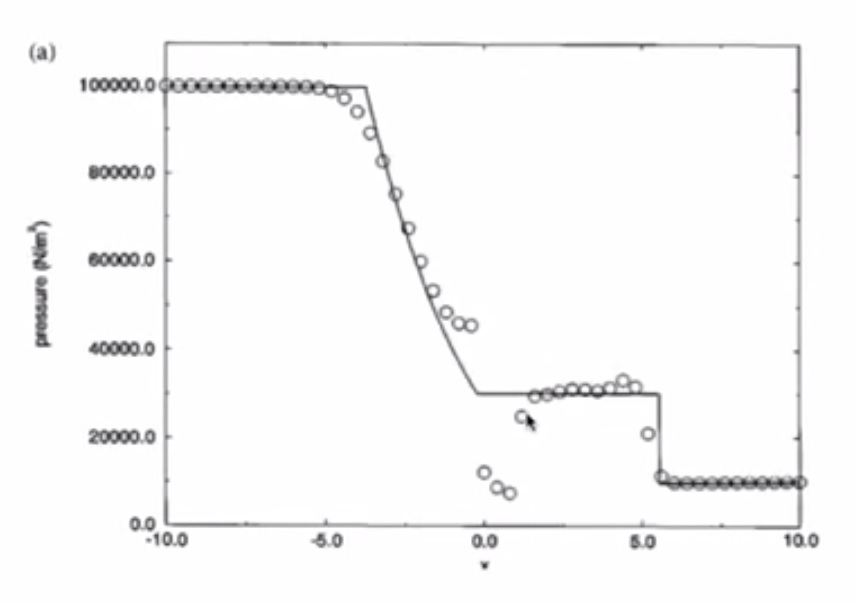
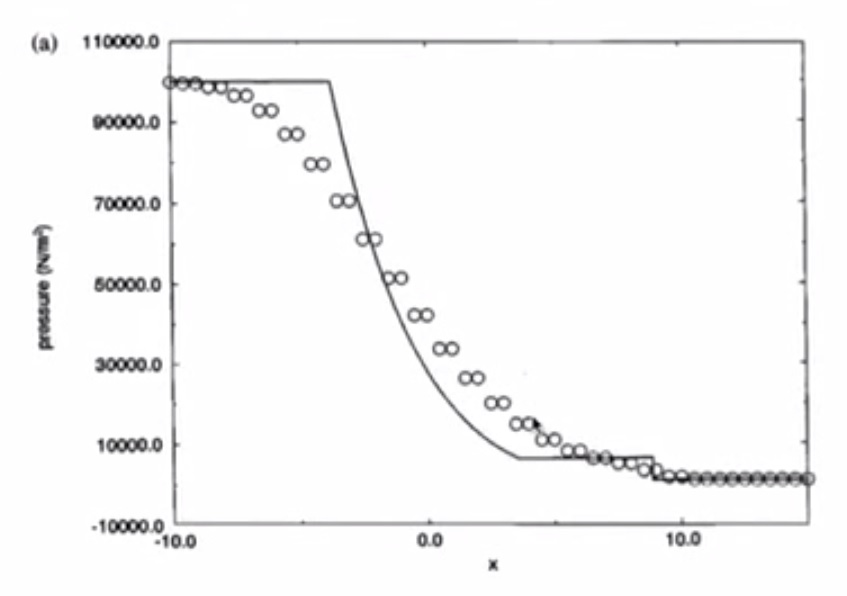
- Pressure
- Velocity
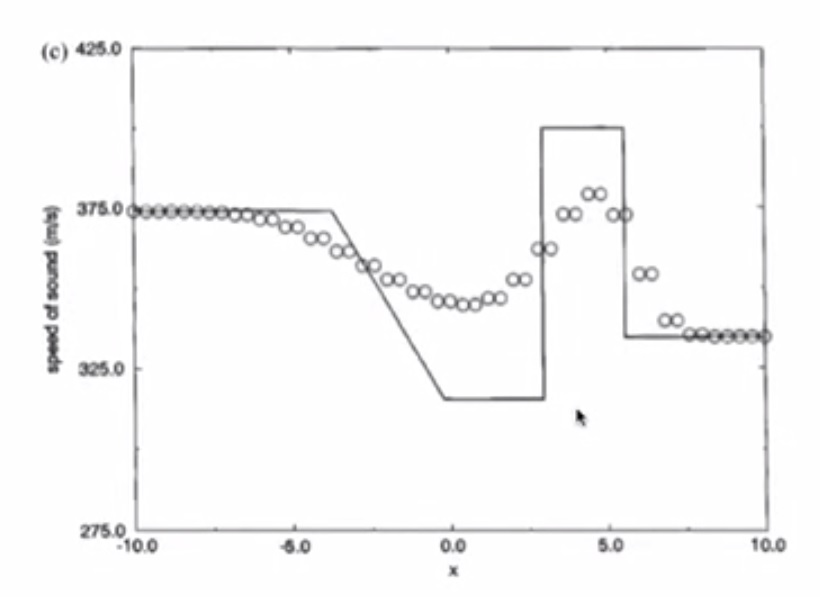
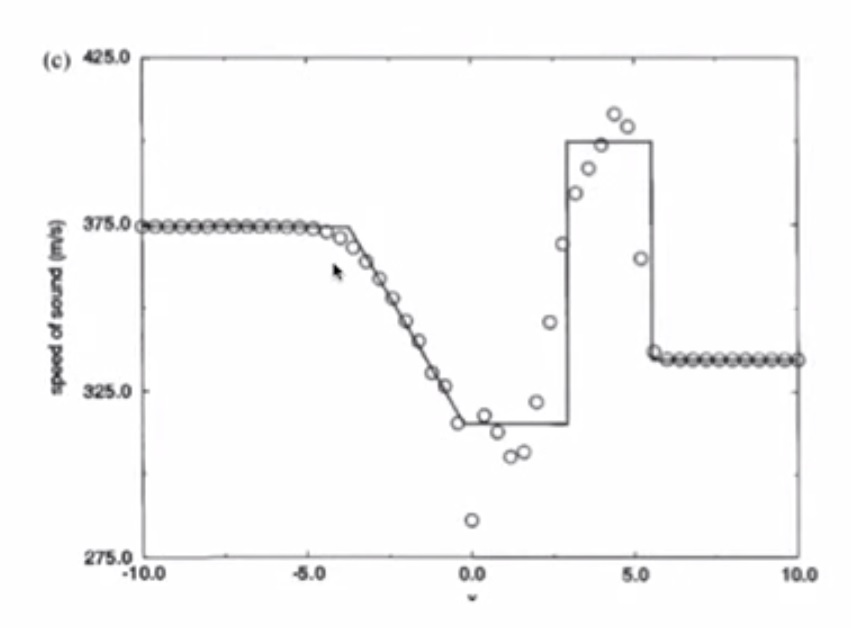
- Speed of sound
- Density
- Entropy
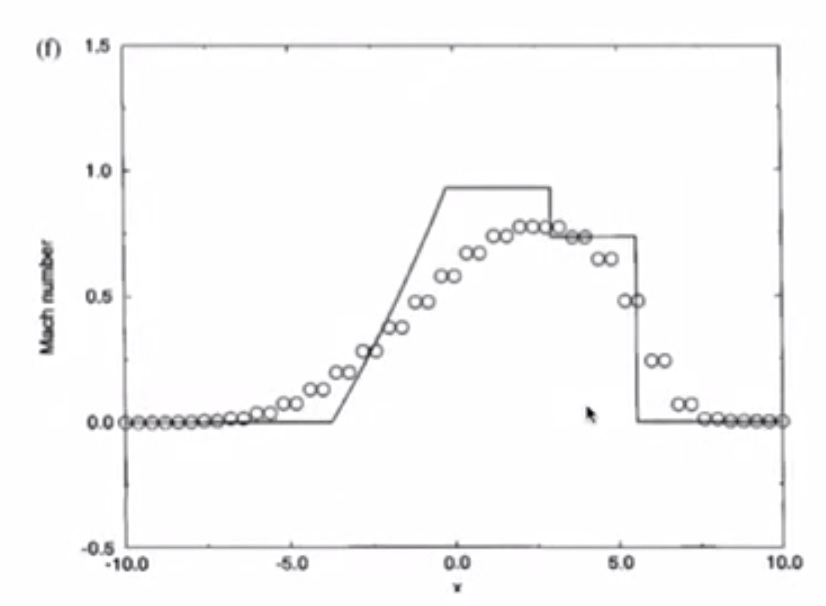
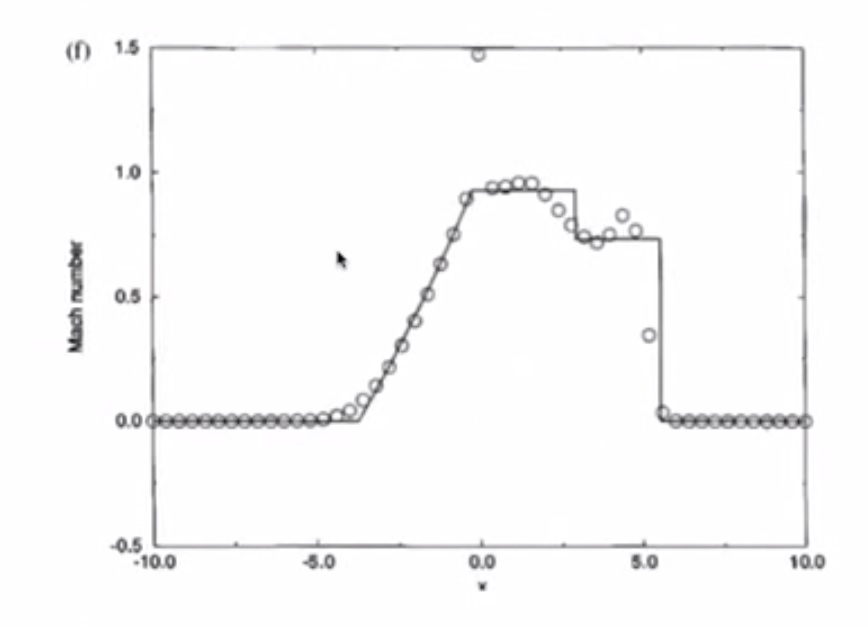
- Mach Number
Can also use Euler Equations in Primitive Form with:
- Pressure
- Velocity
- Density
Vector notation for the Euler Equations with Primitive Variables, \(p, u, \rho\)
4.4.1. Initial Conditions¶
- Everything is quiet until you break the diaphragm (u=0)
- The pressure ratio is 10
4.4.2. Discretisation¶
- N = 50 points in [-10m, 10m]
- \(\Delta x\) = 20m / 50 = 0.4m
- Initial CFL = 0.3
- Initial wave speed = 374.17m/s
- Timestep \(\Delta t\) = 0.4(0.4/374.17) = 4.276 \(\times 10^{-4}\)
- \(\Delta t / \Delta x\) = 1.069 \(\times 10^{-3}\)
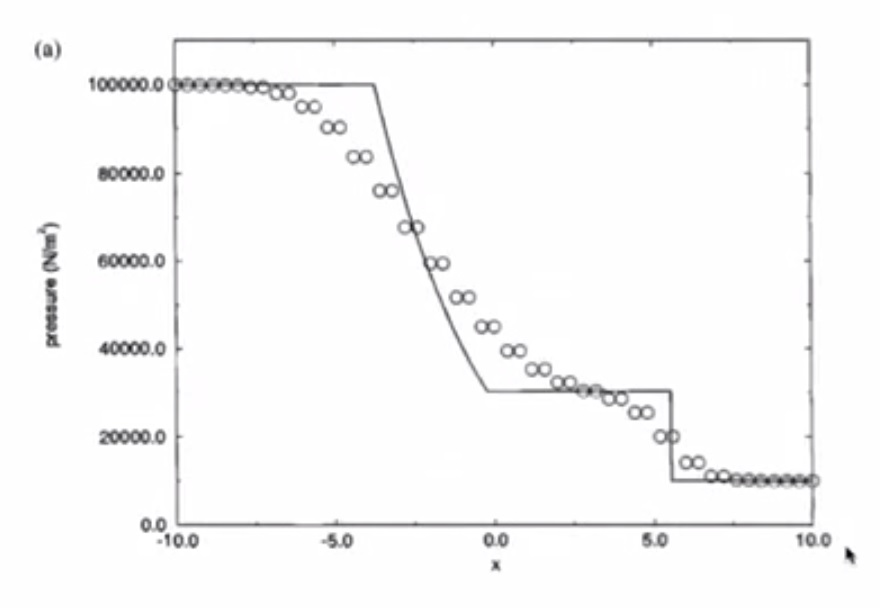
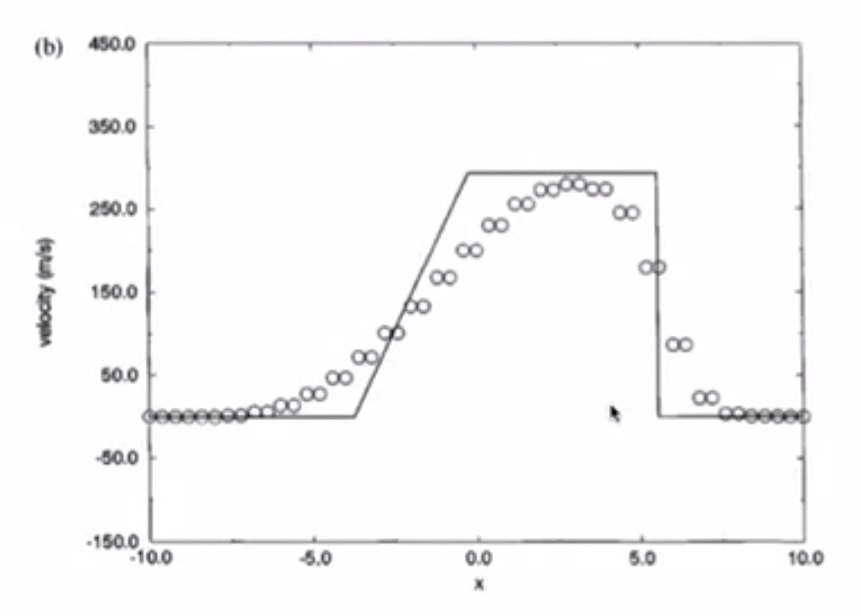
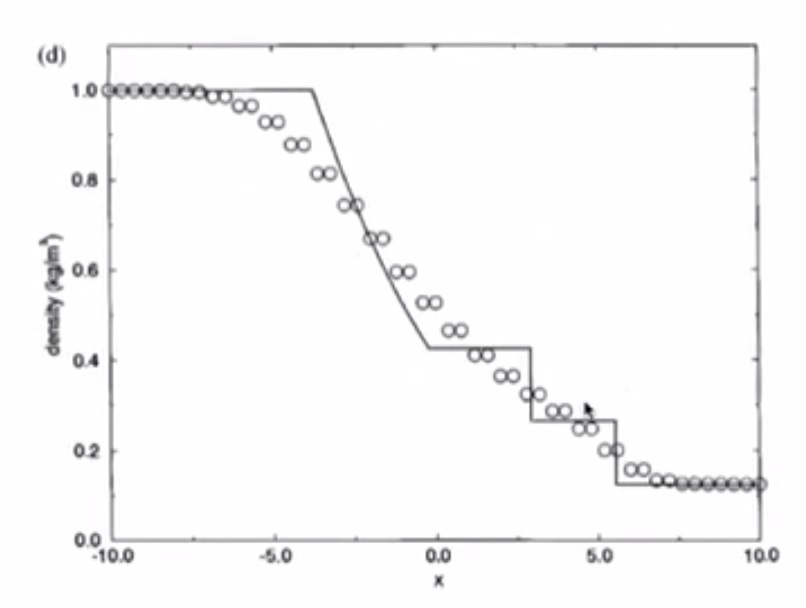
Solution at t = 0.01s (in about 23 timesteps)
Now the problem is described, the numerical schemes can be applied.
4.5. Sod’s Test Number 2¶
Unknowns are same as Test Number 1
4.5.1. Initial Conditions¶
Pressure ratio is 100 - this test is harder
4.5.2. Discretisation¶
- N = 50 points in [-10m, 15m]
- \(\Delta x\) = 25m / 50 = 0.5m
- Initial CFL = 0.3
- Initial wave speed = 374.17m/s
- Timestep \(\Delta t\) = 0.3(0.5/374.17) = 4.01 \(\times 10^{-4}\)
- \(\Delta t / \Delta x\) = 8.02 \(\times 10^{-4}\)
Solution at t = 0.01s (in about 25 timesteps)
Now the problem is described, the numerical schemes can be applied.
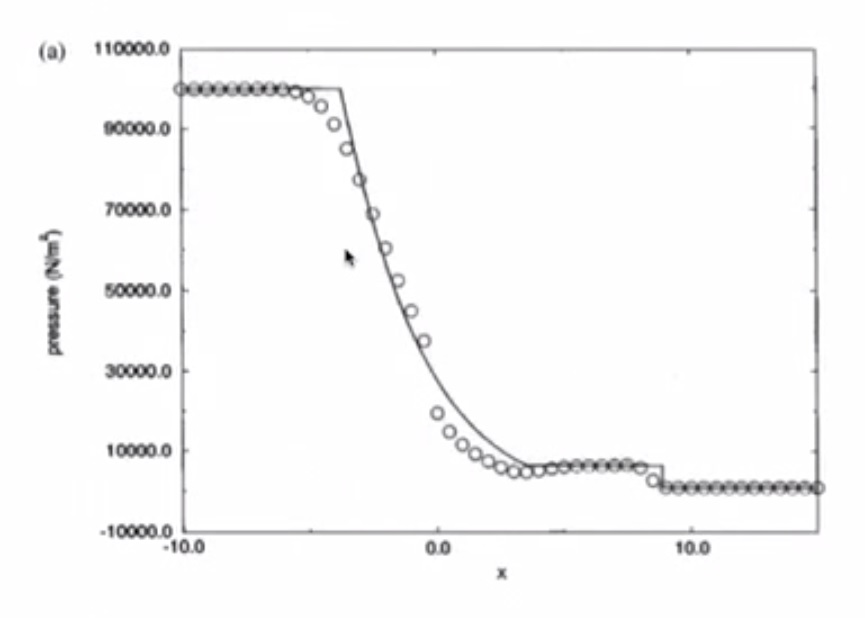
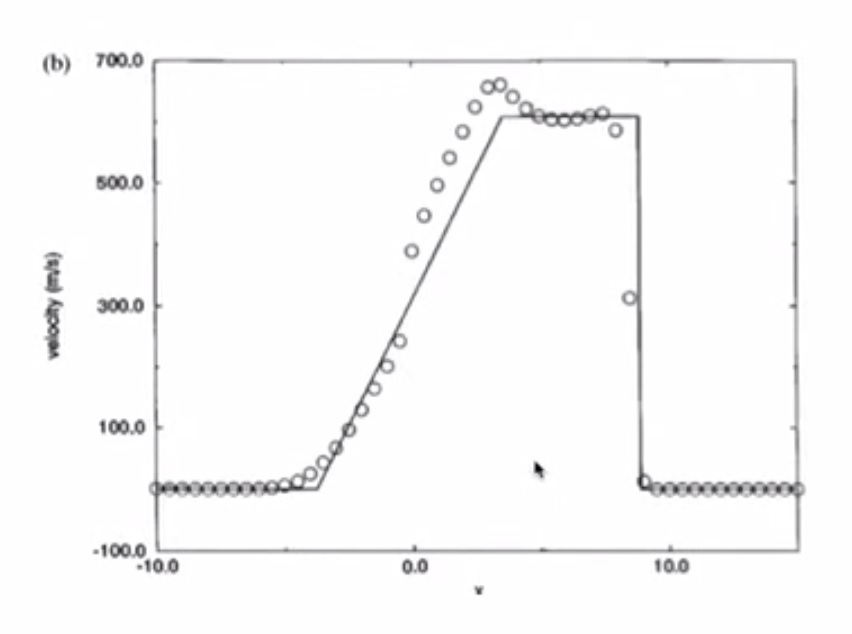
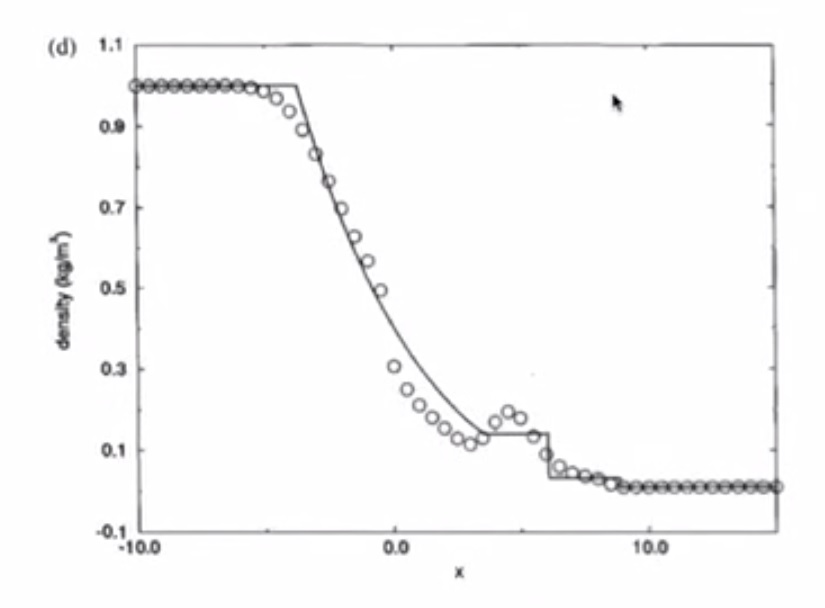
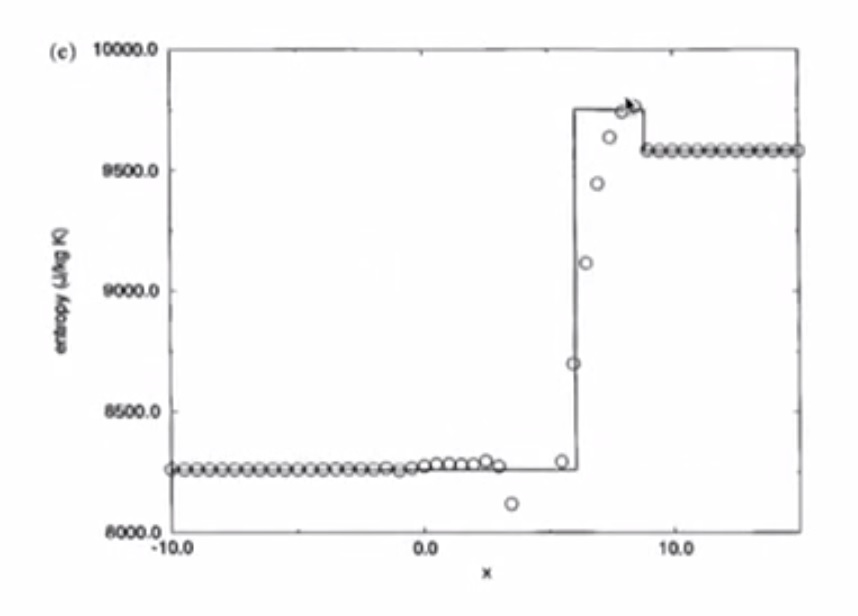
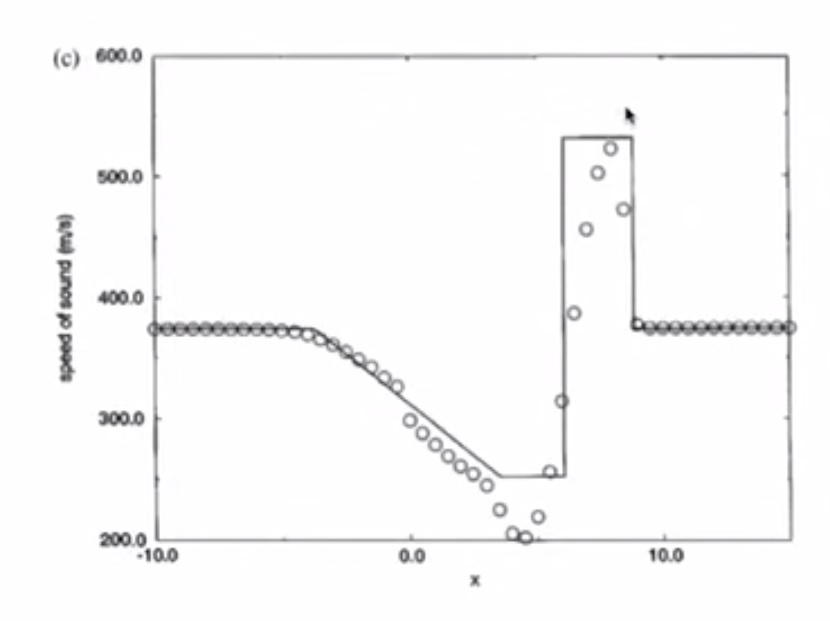
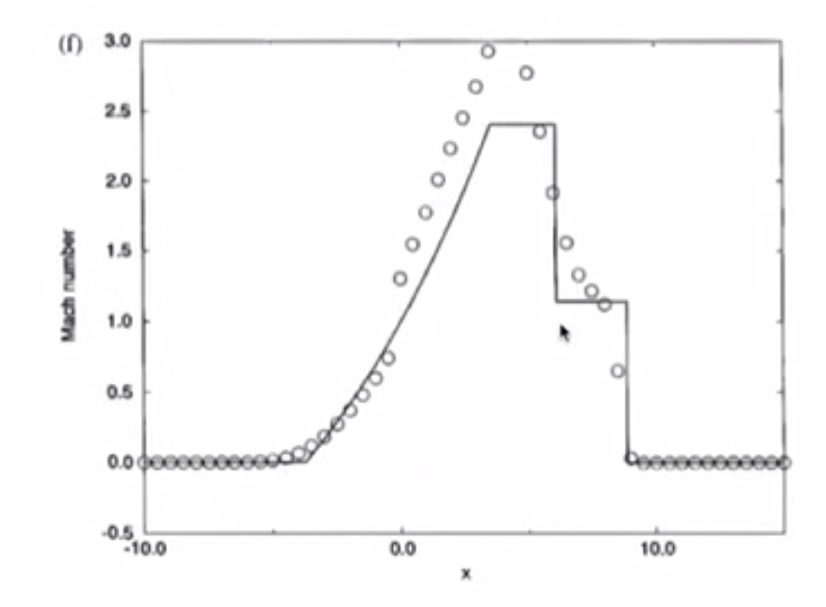
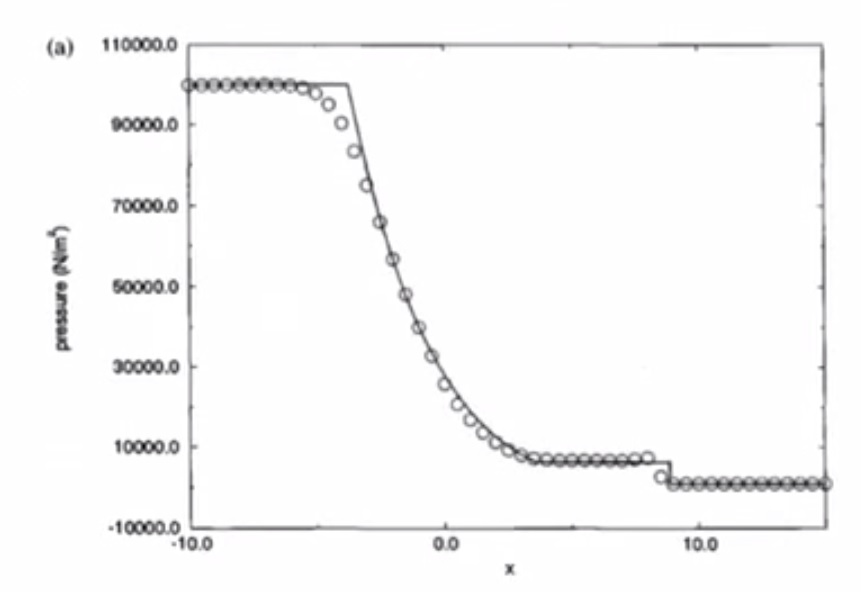
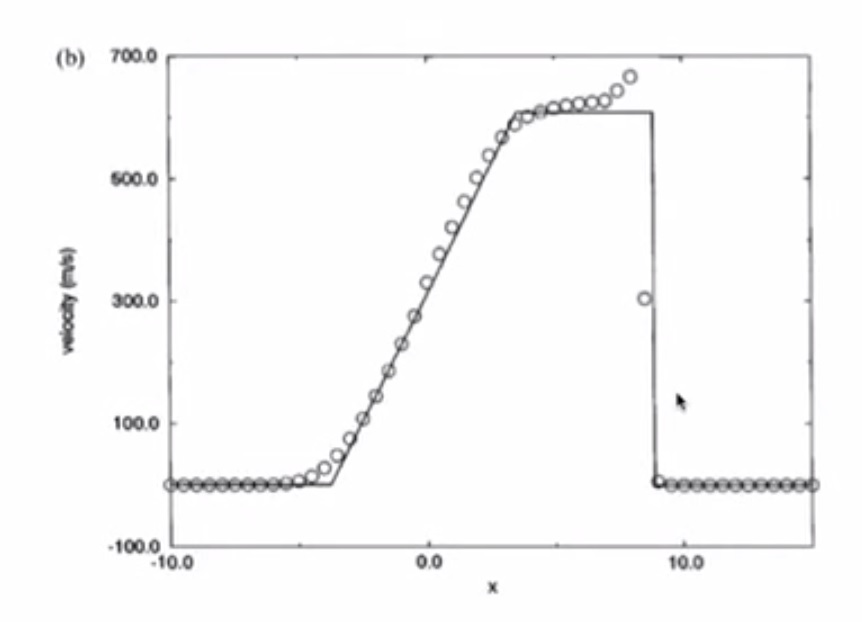
4.6. Test 1¶
4.6.1. Lax-Friedrichs¶
- Pressure has a jump due to shockwave
- Solution has numerical dissipation
- Odd-even decoupling is present (staircase pattern)
- Burgers Equation simulated all the important features of the Euler Equations
4.6.2. MacCormack¶
- Similar to inviscid Burgers
- Overshoot in pressure, speed of sound, density, entropy is bad
- Lax-Friedrichs is better than MacCormack
4.6.3. Richtmyer¶
- Less overshooting than MacCormack
- Undershoot in pressure is bad
- Overshoot in velocity is bad
4.7. Test 2¶
4.7.2. MacCormack with Artificial Viscosity¶
- Smaller amplitude of oscillations even in Test 2
- Small number of points - is a hard test for numerical scheme (coarse mesh)
- Overshoot in velocity
4.7.3. Richtmyer with Artificial Viscosity¶
- Nice result - better than MacCormack
- Smaller about of overshoot
- No oscillations in density - negative density might result in mass not being conserved
4.8. Conclusion¶
- Conclusions from Burgers Equation apply to Euler Equations
- This is the usefulness of the model equations